Cryptography in Blockchain
Topics
Encryption and Bitcoin
No right of private conversation was enumerated in the Constitution. I don't suppose it occurred to anyone at the time that it could be prevented.
The reference of the Bitcoin source code provides implementations of both a node and a wallet. The wallet is responsible for generating and storing public and private keys, through which the node can encrypt and decrypt messages, allowing the user to send and receive bitcoins.
Its implementation of the wallet uses AES-256 and is
called crypto/aes. Independent developers can use the reference implementation to
create wallets in the form of mobile apps, web wallets, or even hardware wallets.
Encryption however isn't part of the Bitcoin protocol as its akin to a public, distributed ledger and data flows within the network unencrypted. Blockchain, however, uses hash functions to ensure that the data is not tampered with ("signature"), an idea that we will explore in much greater depth in the following sections.
Readers are encouraged to complete the Cryptography 101 chapter before continuing.
Hash Functions
As compared to encryption functions, hash functions are irreversible (one-way), keyless, fixed-sized, and serve to validate the integrity of data. While encryption preserves the original text fully, hashing produces a fixed-length signature of the original text.
On a high level, this is how we could use hashing:
- Write our message to a file
- Use a hashing algorithm like MD5 or sha256 to hash the message
- Store the hash in a file and optionally encrypt it with the private key resulting in a digitally signed message
- Send the message to the recipient
- Recipient verify the hash by comparing it to the hash stored in the file
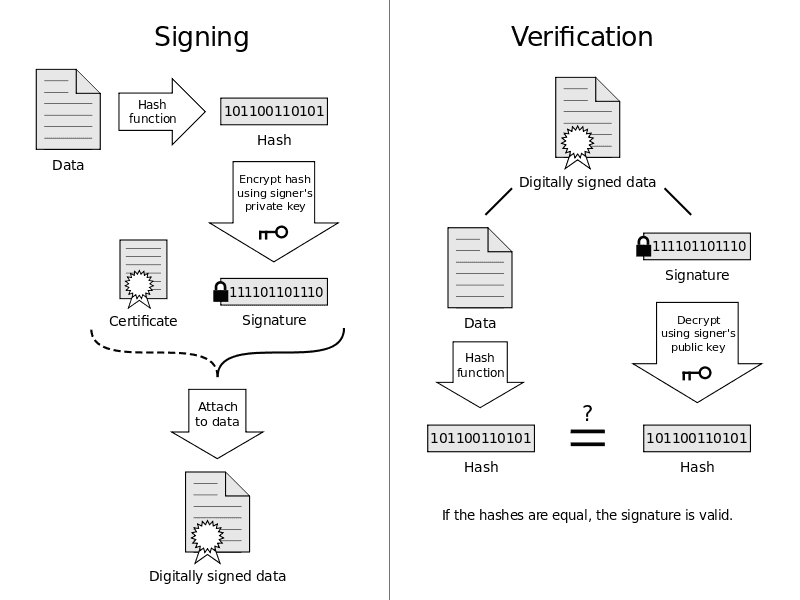
A quick visual diagram of that process looks like this:
Hashing with md5sum
We could have substituted step (1) in the example above, and generalize it to let's say, web software.
If Alice is asked to install Google Chrome on her computer, she would have to first download the browser off an online source. Many internet sites happily host a version of Chrome online in the hope that the web traffic could make up for some advertising revenue. How would Alice be assured that the Chrome browser she installed has not been tampered with?
Well, it turns out she can check the hash of the software she downloaded. One such standard is the MD5 hash, which is a 16-byte hash function. The 'MD' in MD5 stands for Message Digest.
After downloading (but before executing the installer),
she can look into the package for a file containing the hash (on Linux, typically in a location like
/var/lib/dpkg/info/google-chrome.md5sums). In fact, this operation is so common that most OS ships
with some sort of hash checking tool. A Ubuntu user can hence find the list of files with checksums
in /var/lib/dpkg/info/<package_name>.md5sums. Here's an example for my Python3 installation:
edace46345e940177c40892e87457393 usr/lib/valgrind/python3.supp5d52ee1b68c656621c6e2245d07f174c usr/share/doc/python3/copyright3095c50e86c4e6b04e7d178bc936ac70 usr/share/doc/python3/python-policy.dbk.gzfce588a7b0f9617ef102dba9459c7772 usr/share/doc/python3/python-policy.html/build_dependencies.html52e29e520566050cbbc7dacebca223bf usr/share/doc/python3/python-policy.html/embed.html128379472666538c7655e0c8ca3a29f4 usr/share/doc/python3/python-policy.html/index.htmlf4469eeb667e6f11d99f69ee3e383d1f usr/share/doc/python3/python-policy.html/module_packages.htmle1b6ec3e3263267076434e4d3e14aae8 usr/share/doc/python3/python-policy.html/packaging_tools.htmlc5dcbce05b95304c5e343176a6542e51 usr/share/doc/python3/python-policy.html/programs.html3e64ba4e2ba59b3227268fafdb2ee557 usr/share/doc/python3/python-policy.html/python.htmlfaa21ee45374f12459d7979924094b37 usr/share/doc/python3/python-policy.html/python3.html...
I can also use dpkg -V to verify the integrity of the package by comparing the hash
it found with the database metadata.
V, --verify [package-name...]Verifies the integrity of package-name or all packages if omit‐ted, by comparing information from the installed paths with thedatabase metadata.
If md5sum is installed on your system, you can use it to generate the hash of a file. Alice
could write a note, save it as message.txt and generate the MD5 hash using the command:
md5sum message.txt >> message.md5sums
When Bob receives this message, he can verify the integrity of the message by comparing the hash to the one he generate from the message following the same procedure. If even a single character has been modified, the hash output should be completely different (a property sometimes referred to as an "avalanche effect").
Open source projects like R rely on community support for the hosting of their software, and often provide instructions on their installation page to verify the integrity of their software. For example, the first paragraph on the R installation page says:
If you want to double-check that the package you have downloaded matches the package distributed by CRAN, you can compare the md5sum of the .exe to the fingerprint on the master server. You will need a version of md5sum for windows: both graphical and command line versions are available.
Security properties of hash functions
- Fixed length: the hash function is fixed-sized, and thus can be used to generate a fixed-length signature.
- Pre-image resistance (One way): the hash function cannot be used to generate a pre-image of the message.
- , where is the message and is the hash. is a pre-image of and cannot be reverse-computed from .
- Collision resistance: Different input message should result in different hash, that is
- It is impossible to fully avoid collisions in hashing functions (compression down to 32 bytes, hence subjected to the same problem as a "birthday function") -- but sufficienctly long collisions are computationally infeasible to find.
Secure Hash Algorithms
Message Digest functions such as MD5 is no longer considered to be cryptographically secure and what you'll find more readily recommended today are SHA algorithms. SHA-256 is a 256-bit hash function, which has 32 bytes of output and belongs to the Secure Hash Algorithms (SHAs) family.
We spoke of the importance of integrity checks, but hashing functions have wide-ranging applications beyond that. For example, producing hash tables can quite substantially improve the query performance while using less desk spaces. Hashes can also be used by cybersecurity teams to fingerprint a file, identify a file's origin, or fingerprint a known malware / virus without having to scan the entire file. Peer-to-peer networks for file sharing also relies on hash functions to ensure that files are not corrupted.
In blockchain, the proof of work algorithm uses SHA-256 as the hash function to verify the computational work done by miners.
Let's take a look at the SHA family of hash functions, starting from SHA-1 commonly used in SSL and TLS implementations until browser vendors ceased acceptance for it in 2017.
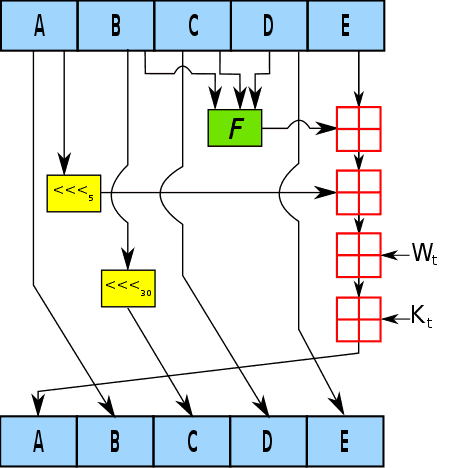
SHA-1 takes a message of arbitrary length and produces a 160-bit hash value, that is, 160 binary bits of 0 and 1 represented as a 40-digit long hexadecimal string. A quick inspection on one iteration used in the SHA-1 algorithm shows that the 160-bit hash value is generated by the following steps:
- The message is padded with a single '1' bit followed by as many '0' bits as necessary followed by the message length, to make the length of the message a multiple of 512 bits.
- The message is then split into 512-bit blocks, and each block is chunked into 16 32-bit words.
- We have an internal state of the SHA-1 algorithm, which is initialized to the following values:
- A = 0x67452301
- B = 0xEFCDAB89
- C = 0x98BADCFE
- D = 0x10325476
- E = 0xC3D2E1F0
- This internal state is exactly the same length as the hash output, which is 160 bits. (A through E has 32-bit each)
- In an iterative process, we will update the values of A through E
- We then incorporate the message () along with a nonlinear function ()
- Other notations:
- denotes a left rotation by bits
- is the round constant of round
- denotes adddition modulo 2^32
- At the end of each round, the resulting values of A through E are used to update the internal state. They would be the new values for A through E in the next round.
A couple of observations are worth mentioning. Additions in SHA are done with modulo , which avoids overflow in the arithmetic. This has the effect of making the overall hashing algorithm a one-way function (pre-image resistance) even if an adversary understood the intricacies of the algorithm.
For example, supposed an input numeric of 12345, mod 16, resulting in 9. Given 9 and given the formula , the pre-image candidate is still an infinitely long list of 25, 41, 57 ... Supposed the hashing algorithm is as simplistic as just a modulo operation though, now we succumb to high collision rates. Fortunately, we've incorporated length extension into the algorithm, which is a technique called "padding". We pad the messages with 1, followed by as many 0 as required (plus the bitlength of the entire message) to make the length of the message a multiple of 512 bits.
This repetitive updating of the internal state with a compression function is based on the Merkle-Damgard construction, which we'll discuss below.
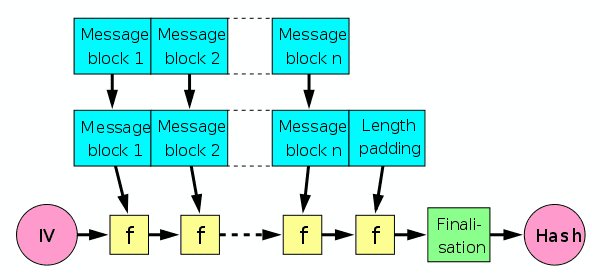
Merkle-Damgard construction
SHA-1, like SHA-0 before it and SHA-2 after it, uses Merkle-Damgard construction, a popular construction used in many cryptographic hash functions.
Merkle-Damgard construction divides the input data into equal sizes of blocks and then applies a compression function to each block. The output of the compression function of each block is then hashed together with the output of the compression function of the previous block. This process is repeated until the final hash is obtained.
- is the compression function, and transforms two fixed-length inputs to an output of the same size as one of the inputs.
- is initialization vector, which is a fixed value specific to the algorithm or implementation.
- The finalisation step is the same as the compression function, but incorporates the length of the message ("length padding") to deliver better mixing and an avlanche effect.
One reason for its popularity and its use in all collision-resistant hash functions is the theorem that if is collision-resistant, then the overall hash function constructed using it is collision-resistant -- proven by Merkle and Damgard.
We've established that the SHA family of hash functions use Merkle-Damgard construction, and we've seen its pre-image resistance property, but another detail of note is the effect of the length padding. SHA-1 always pads the message, even if the message is already a multiple of 512 bits.
Consider what should happen if a message of the right length () is not padded, while another message of a length not in the multiples of 512 () is padded. This would lead us to a collision since .
Consider also a strategy that pads the message with a constant string of 0s until it is of the right length. That, too, will lead to a collision .
So by employing the two padding strategies, SHA-1 can avoid collisions (up to a certain extent).
With that in mind, head into the following Experiment and play with the hash function implemented for you.
Experiment 1
SHA family of hash functions
- Go ahead and type your first name into the field below.
- Change one character in your name, and observe the hash change.
- Notice that even a minor change (an extra space, or a capitalized letter) results in an entirely different hash ("avalanche effect").
- Observe that a SHA256 hash is fixed-length whether your name is 120 characters long or 3 characters short; You'll always get a hash that is 32 bytes long, comprising of 64 hexadecimal digits.
The experiment above also demonstrates how password hashing is used in the real world. A good security practice is to use a hash function to generate a one-way hash of the password, and store the hash in the database instead of the plain text.
When a user attempts to make a legitimate login again, they would enter the password on, say, a web form, and the hash of which is thus compared to the one stored in the database. A passed equality check would indicate that the password is correct and that the user should be authorized.
It should also be noted that precomputed table that caches the output of cryptographic hashes (known also as a rainbow table) for common strings exists and are quite readily available. A hacker can thus use these pre-computed values, up to tens of millions of them at a time, to crack passwords in a dictionary attack.
SHA-2 and SHA-3 (Keccak)
SHA-256 belongs to the SHA-2 family and it generates a 256-bit (64 hexadecimal digits) hash value. It is more secure than SHA-1, and similar to how SHA-1 uses an internal state size consistent to its output size, so does the SHA-256, giving it an internal state size of 256.
SHA-256 in considered to be vastly more secure than SHA-1, and has been adopted by many cryptographic protocols, including TLS and SSL (replacing SHA-1) in the recent years. SHA-256 is used by the Bitcoin protocol.
SHA-3 was developed in late 2015 by the Keccak team, or rather, it is the NIST-standardized version of Keccak. The submission must meet the requirement of supporting at least 4 variants, so the team submitted the following variants supporting different fixed-lengths outputs:
- SHA3-224: 224-bit output
- SHA3-256: 256-bit output
- SHA3-384: 384-bit output
- SHA3-512: 512-bit output
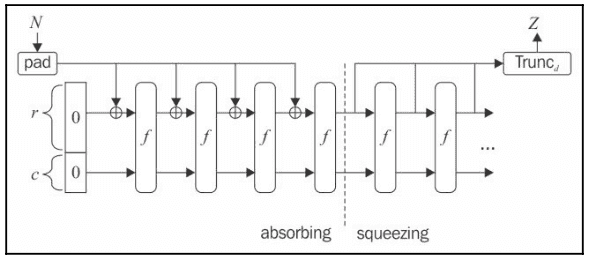
It has not seen widespread use yet and its design differ from that of SHA-1 and SHA-2. Notably, Keccak does not make use of the Merkle-Damgard construction, but instead uses what is known as the sponge construction.
While we've learned that AES has a block size of 128 bits ("state size"), consider that Keccak has a state size of 1600 bits (think , considerably larger -- and more secured).
The 1600 bits of state size are divided into and following the allocation below:
| Type | Output (bits) | Bitrate (r) | Capacity (c) |
|---|---|---|---|
| SHA3-224 | 224 | 1152 | 448 |
| SHA3-256 | 256 | 1088 | 512 |
| SHA-384 | 384 | 832 | 768 |
| SHA3-512 | 512 | 576 | 1024 |
Another parameter is the number of rounds, which is determined by where state size is a function of .
Since Ethereum uses KECCAK-256, we'll use the 256 variant here to illustrate the key ideas of the algorithm. With state size of 1,600, would be 6. Rounds is then 12 + 2*6 = 24.
Assuming SHA3-256 is used, these are the notations:
- Absorbing phase:
- controls the number of bits we are going to process in each round (1,088), and is used to perform the XOR operation with the message block
- controls the capacity level, in our case of SHA3-256 it's 512.
- and sums up to a length of 1,600 bits and is a vector of all 0s.
- Our message is chunked into bits of 1,088 (), with padding added at the end to make the message a multiple of 1,088 bits
- The first chunk is fed into an exclusive-or () operation; In this case, we XOR-ed the first 1,088 bits of message with a 1,088-bit long vector of all 0s.
- We then feed this into a permutation function () which uses XOR, AND and NOT operations for easy implementation. This permutation function is repeated for 24 rounds (see above).
- The result of the permutation (also length of 1,088) is then fed into the next exclusive-or operation along with the next 1,088-bit chunk of message. is not XOR-ed and carry over into the next permutation.
- The above process makes up the "absorbing phase" of the sponge construction, which gets its name from the fact that it absorbs the message while defining / shaping the internal state.
- After the absorbing phase (meaning we've fully consumed the message), we move into the "squeezing phase", where we again put it through the permutation function
- We need to output 256 bits, so we truncate the output of the permutation function (take the first 256 bits) and output , our digest / hash value.
- For different selection of rate () and type), the output length of the permutation function will be different so repeat the process as necessary until the desired length for is reached.
Digital Signatures Algorithm
In the next experiment, you will put into practice many of the concepts you've learned in the previous sections. We are going to create a public and private key pair, and then sign a message with the private key.
Your public key will be broadcasted to everyone, and your private key will be kept private. Anyone in a peer to peer network can use your public key to verify the signature of the message, and hence establishing the authenticity of the message. In other words, anyone can verify that a blockchain transaction originating from your wallet to another's is indeed initiated by you.
Diffie-Helman Key Exchange
This idea is first introduced in the earlier chapter on public key cryptography. In it, we've learned how any sender can sign the message using their private key before transmitting the message along with the signature to the receiver. Anyone can verify the integrity of this message using the public key of the sender.
We've seen an example of this in the previous chapter, where we used the RSA algorithm to create a public key. RSA works by relying on the fact that large prime numbers are difficult to factor (the integer factorization problem).
Another way to develop public key algorithms is based on the idea of the discrete logarithm problem, which describes how computationally infeasible it is to find the exponent of the generator. The Diffie-Helman Key Exchange algorithm makes use of this problem, which is described as follows:
- Alice and Bob agree publicly on a prime modulus and a generator. The generator is also a primitive root of the prime modulus and
they're selected this way to ensure that the resulting shared secret can take on any value from 1 to .
- The prime modulus they agreed on is 31 (), and the base is 3 ()
- Alice chooses a secret integer and Bob chooses a secret integer .
- Alice's secret number is 13.
- Bob's secret number is 17.
- Alice and Bob perform the calculation and send the result to each other.
- Alice sends Bob the number 24:
- Bob sends Alice the number 22:
- Upon receiving the number, each of them perform the calculation where is the received number and is the secret number
- Alice computes
- Bob computes
- They now arrive at the same number , and this is the secret they use as an encryption key for sending messages across the network.
Notice that a is known only to Alice, and b is known only to Bob. Additionally, one can also observe that the final calculation Alice makes are equivalent to the final calculation Bob makes
- Alice:
- Bob:
The exponents are ordered differently but that doesn't change the result, and so in effect both Alice and Bob performed a calculation that involves raising the to the power of both their secret numbers without ever knowing the other's secret number.
Using the discrete logarithm problem this way to create a public key isn't exclusive to the Diffie-Helman Key Exchange algorithm. Elliptic curves (an algebraic cubic curve over a field, such as the field of real numbers or prime finite fields) are also used to create public keys. What RSA does with prime numbers, elliptic curve cryptography (ECC) does with elliptic curves, and the two are very similar. Notable schemes in ECC are Elliptic Curve Diffie-Hellman (ECDH) for key exchange and Elliptic Curve Digital Signature Algorithm (ECDSA), which is based on the idea of signing a message with a private key and verifying the signature with the public key.
Experiment 2: ECDSA
In the following experiment we will be creating a public and private key pair using Secp256k1, the specific ECDSA algorithm used in Bitcoin. All points on the curve are valid Bitcoin public keys, generated by taking a random 256-bit number ("private key") and multiplying it by the generator point before returning the coordinates of the resulting point.
Due to the discrete log problem, dividing by the generator point is not possible, which gives it the desired property of being intractable.
Instructions
- Create a private key and public key pair using the Secp256k1 curve
- Write a plain text message and sign it with the private key. This message is a representation of what could be a transaction of some sort on a blockchain
- Take note of the signature that was generated when you sign it with your private key
- Your private key will remain private but your public key will be broadcasted to everyone. Anyone in a peer to peer network can use your public key to verify the signature of the message, and hence establishing the authenticity of the message.
- Try to have a failed verification by entering a different message and/or signature. Changing even a small punctuation, or capitalizing a letter will invalidate the signature. This is the mechanism that keep transactions honest and secure, for as long as private keys remain secret.
Public and Private Keys
Private Key:Public Key:Signing
Merkle Tree
Merkle Tree is a concept in cryptography and computer science introduced by Ralph Merkle in 1974. It is the same Merkle who invented the Merkle-Damgard construction. Every node in the tree (except the "leaf") has two children, and the value of each node is the hash of the values of its child nodes. When visualized below, we get a sense of how Merkle Trees are efficient structures for secure verification of contents -- even of large sizes.
In terms of application, Merkle Trees are used to ensure that data ("blocks") received from participants in a peer-to-peer network ("peers") are valid and not tampered with. A peer that sends a block that has been altered will be rejected since its hash will not match the Merkle Tree's root ("root hash"). Its application includes Git and Mercurial (revision control systems), and is used in the blockchain protocols such as Bitcoin (and by extension its forks, e.g Bitcoin Cash) and Ethereum.
The famed Bitcoin inventor Satoshi Nakamoto wrote about Merkle Tree and cited Ralph's paper in the references for the Bitcoin whitepaper. It is perhaps safe to say that Merkle Tree is foundational to a peer-to-peer blockchain architecture, the absence of which render the trustless consensus mechanism infeasible.
Experiment 3: Merkle Proof
One of blockchain's central tenet is the idea of a trustless infrastructure. "Don't trust. Verify." is an often cited statement, and is well embedded in its design. To fully mitigate trust in a third party mediator, each node in a blockchain must be able to verify the record of all transactions independently, but doing so may incur a huge computational cost if not for the merkle proof mechanism.
Instructions
Create a Merkle Tree that maps donors (through "username") to their donation amounts. Start with 3 donors, but feel free to repeat the experiment with as many donors as you want.
Observe the Tree Representation. Supposed you entered "alice" and "100" for the Username and Donation Amount respectively, internally the experiment concatenate them to
alice +100and then hashes it with SHA256. Because SHA256, as a cryptographic hash function, is a deterministic function, the hash of the concatenated string is the same for every execution of the experiment. In fact, if you insertalice +100into Experiment 1, you'll obtain the same digest as the one you get here.Modify the donation value or any one character of the donor's username (hit 'Construct' to reconstruct the tree), and observe the avalanche effect running through the node to the root of the tree.
Nodes (excluding leaf nodes) are hashes of their children.
Hash(0)is computed bysha256(hash(0-0) + hash(0-1))and so on. An implementation detail here is that this concatenation is performed on the byte sequences -- hash functions operate on bytes, i.e it takes it bytes and return bytes. Because of this, while we represent the byte sequence in hexadecimal characters (0x) for readability, we perform the concatenation operation on the two byte sequences and not on their hex digests.
#### 1. Compute sha256 for each child node to get its binary digest###bin_a = '01100001011011000110100101100011011001010010000000101011001100010011000000110000'hex_a = "{0:0>4X}".format(int(bin_a,2)) # 616C696365202B313030m_a = binascii.a2b_hex(hex_a) # b'alice +100'h_a = sha256(m_a).hexdigest() # 'dc2cac4a8aaeccc0199eeb77df68b22eaa6e319d3f2b425d078dbd73419e28ac'dig_a = sha256(m_a).digest() # binary codem_b = b'bob +50'h_b = sha256(m_b).hexdigest() # 7e15e5bc1b84f458db7ced4df762ba70204f19e3a613738756f9b00653f0aee1dig_b = sha256(data2).digest() # binary code#### 2. Finally, sha256(digest of child nodes concatenated)###sha256(dig_a+dig_b).hexdigest()# 'edf9a9a0e56b58fc9caccb97d85c628d5b9dc50cb94dfc41e83026d37704400f'
Because the operations are performed on the binary code, the concatenation is thus the addition of two sequence of bytes.
dig_a = sha256(m_a).digest() # b'\xdc,\xacJ\x8a\xae\xcc\xc0\x19\x9e\xebw\xdfh\xb2.\xaan1\x9d?+B]\x07\x8d\xbdsA\x9e(\xac'dig_b = sha256(data2).digest() # b'~\x15\xe5\xbc\x1b\x84\xf4X\xdb|\xedM\xf7b\xbap O\x19\xe3\xa6\x13s\x87V\xf9\xb0\x06S\xf0\xae\xe1'# the + is just simple concatenation# b'\xdc' + b'~\x15' => b'\xdc~\x15'
- To validate that a donor has in fact donated said amount of money to a given fundraiser, we need to perform what is known as an inclusion proof. Using the Merkle tree, we need only the data we're attempting to prove, and the sibling hashes along the path to the root.
h_abcdh_ab h_cdh_a h_b h_c h_d
In the example tree above, to prove inclusivity of d, we need only to know h_c and h_ab.
We then compute the hash root and compare our computed value to the actual Merkle root. We need not know the values of other nodes
outside this path to the root, hence allowing us to do this verification in time
where is the number of nodes in the tree, as well as requiring only hashes
to be transmitted for the proof.
- Before you move on from this exercise, consider one more scenario.
Supposed we have two merkle trees(
AandB), both with a parent node and two children nodes.
- Merkle tree
A's left children node is 'alice +100' and its right children node is 'alice -20'. - Merkle tree
B's left children node is 'alice -20' and its right children node is 'alice +100'.
### Merkle tree Ah(h(a +100) + h(a -20))h(a +100) h(a -20)### Are they equivalent?### Merkle tree Bh(h(a -20) + h(a +100))h(a -20) h(a +100)
Would the parent node of A and B be equivalent to each other? In other words, is hash(a+b) the same as hash(b+a)?
This may seem like a trivial question, but it is profound in the context of timestamped verifiable proofs.
Merkle Trees in Bitcoin
SHA-256 is very strong. It's not like the incremental step from MD5 to SHA1. It can last several decades unless there's some massive breakthrough attack. If SHA-256 became completely broken, I think we could come to some agreement about what the honest block chain was before the trouble started, lock that in and continue from there with a new hash function.
Satoshi Nakamoto
In the Bitcoin protocol, double hashing, i.e sha256(sha256(data)) is used in place of the usual sha256(data) to create a merkle tree.
Specifically, Satoshi uses sha256(sha256(data)) in the following places of the implementation:
- The hash function for each block
- The hash function for each block header (
sha256(sha256(Block_Header)))
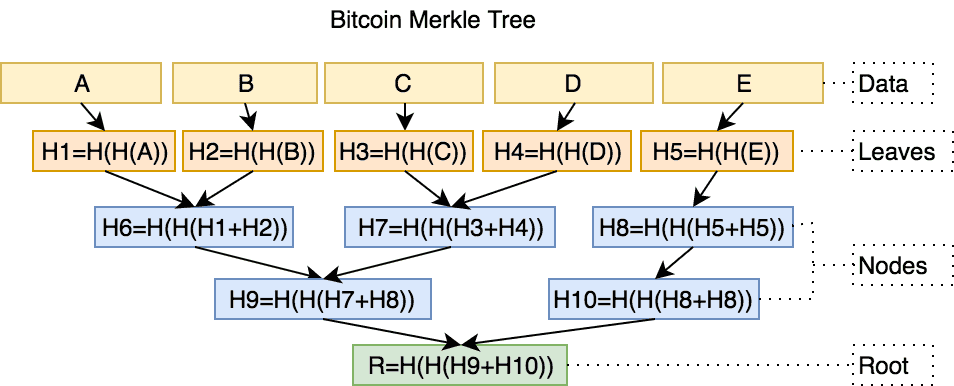 Source: miguelmota/merkletreejs
Source: miguelmota/merkletreejs
Since Bitcoin is an open source project, one can see its source code implementation (line 617) to see how the verification status is checked using the merkle tree.
Exactly why Satoshi chose to do two rounds of hashing is up to debate, but most cryptographers agree that Satoshi believed it was a more secure way to create a merkle tree, particularly in preventing a length-extension attack. That said, existing research doesn't point to any vulnerability in how Bitcoin uses hashes that would make it more susceptible to said length-extension attacks.
A small inaccuracy of the above image is that a Bitcoin Merkle tree assumes an even number of leaf nodes (transactions) to maintain its binary data structure.
If a block contains an odd number of transactions, the last transaction is duplicated to make it even. In the example, the transaction for E is duplicated and hashed
with itself to create a new node.
We allude to the idea of "blocks" but we haven't got to an official definition of what constitutes a block. The following is a brief introduction to this subject and a more in-depth treatment of the Bitcoin protocol is available in the next module of this course.
Bitcoin Blocks
All transactions on the Bitcoin protocol are grouped into blocks (Each block is a collection of transactions) on an approximately 10 minute interval. The block is then broadcasted to the network. Considering the volume of transactions in a block (~ 10 mins), Bitcoin doesn't actually transmit a full record of all transactions in a block, but rather include the Merkle root of that block's transactions in its header ("block header"). Full nodes participants can however obtain the full transactions in a block by sending a separate request.
A curious reader may wonder if we could obtain the same effect by hashing all the transactions sequentially, resulting in a root? This may work, but an inclusion proof will now require hashes to be transmitted, where is the number of transactions. It is expensive memory-wise and considerably less efficient.
In summary, Merkle trees offer the following advantages to a Blockchain implementation:
- Inclusion proof and data integrity checks requires considerably less memory than a sequential hashing approach.
- Less data required to be broadcasted to all nodes in the network.
- A light client (crypto wallet and such) can participate in transaction verification without requiring the computational resources of full nodes since it uses the Merkle root included in each block header rather than the full transaction logs itself. This is a concept known as Simplified Payment Verification (SPV), described in section 8 (titled "SPV") of the Bitcoin whitepaper. It refers to the ability of a transaction recipient to prove that the sender has control of the source funds of the payment intended for that transaction without downloading the full block chain, making use of Merkle Proofs.
Thanks for the key innovation that made SPV possible, light nodes such as mobile-wallet apps can participate in the blockchain without having to request and store 382GB of data. Anyone with a personal computer or smartphone can send, receive, and verify transactions without the capital cost of downloading and storing the entire blockchain.
Knowledge Check
Practical Exercises
- Use the
sha256sumcommand to generate the hash of the filemessage.txt
sha256sum message.txt
Use the Experiment 1 box to generate the hash of a common word or phrase that you suspect to be a weak password. This could be "password" or "secret", or "samuel" or "password123". Try and find a rainbow table or online hash database to match the hash to.
Crackstation or similar services may be used for this exercise.You can use the
sha256sumcommand oropenssl, whichever you have installed to generate the hash of a message. Verify that the values are the same as the one from Experiment 1.
# 1. using openssl dgstecho -n 'supertype' | openssl dgst -sha256# 2. using sha256sumecho -n 'supertype' | sha256sum# 3. does this work?echo 'supertype' > firstname.txtsha256sum firstname.txt
- If you have Python installed, you can use the hashlib module to generate the hash of a message. We can implement a quick and minimal version of the Merkle tree using Python:
>>> from hashlib import sha256>>> def h(s): return sha256(s.encode()).hexdigest()...>>> ha = h('adam +100')>>> ha'6a351a3a0f2e70b51e5c188a8191f94836c149ab07a72d0feb8d5ec6f928bcf3'>>> hb = h('bob +100')>>> hb'd211d3e5157f5e1ca44a588c5ca4679d3c2b61bb5206707189a1ca3587ba8301'
Knowledge Check
You will need to have the appropriate software for this section. More details here.
- The following is the
md5sumandsha256sumof the file[instructions.txt](#):
# md5sum37d84f83de2aed25f06c7536924cf308 instructions.txt# sha256sum778c8537acdc2b3fc7837996f68e9c412509ca5d194b8db5e9929f4f3673ed23 instructions.txt
Verify that, using either hash algorithm (whichever you have installed on your system):
- The file has not been tampered with.
- The hash is incorrect. File has been altered, by even just a single character.
 Learning Modules
Learning Modules